2-D Range Search, Points in a Box Search and K-D Trees

Brute Force

We can split the whole rectangular space into equally sized squares, and store these squares in an ordered list. Each of these squares will carry a set of points contained within.

This works decently if the points are somewhat uniformly spaced. Care needs to be taken on how many squares to subdivide the space into. Too many and you end up with too many empty squares. Too few and then each square contains too many points. A typical choice is to make \(M\times M\) squares, with \(M\) roughly \(\sqrt{N}\).

A bigger problem with this approach is that the points are usually not uniformly spaced. For example, if we subdivide the United States this way, most squares will be empty, as the population is not uniformly distributed.

2-D Trees

A 2-D tree is really just subdividing a rectangle into smaller rectangles using a binary tree. The first node will divide it into left and right subrectangles. The nodes in the next layer will divide each of these subrectangles into top and bottom subrectangles, and so on:

The corresponding tree is:

Now the details on how this is made. The first point is (7,2). We subdivide the rectangle into left and right subrectangles. The next point is (5,4). This subdivides the left rectangle into upper and lower ones. We continue subdividing this way.

How do we choose which point is the root? If you want a balanced tree (which is not always optimal), you pick the “median” point with respect to the axis you’re looking at. If you have too many points and don’t want the expense of taking the median of all of them, simply randomly select a number and use its median.

This is just a binary search tree, but we’re alternating the \(x\) and \(y\) coordinates at each level.

2-D Range Search with 2-D Trees

To do a 2-D range search, we follow down the tree. Whenever we come across a point whose horizontal/vertical line intersects the 2-D rectangle, we need to “mark” it and ensure we traverse both the left and right subtrees. For example, in the diagram above, if the vertical imaginary line going through (4, 7) intersects the rectangle (even if the point is not in it), we need to search both the left and right subtrees as there may be points in each one that are in the rectangle:

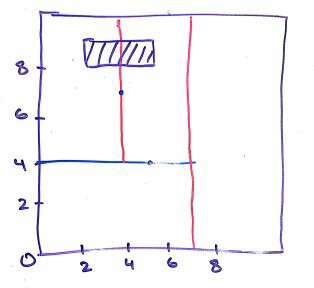
The average run time is \(O(R+\lg N)\) where \(R\) is the number of points in the rectangle. The worst case is \(O(R+\sqrt{N})\) for a balanced tree.

Nearest Neighbor in 2-D

We can use 2-D trees to find the nearest neighbor to a given point. We start at the root of the tree and note the distance to that point. We then go to its child which is on the same subrectangle as the point in question and look at its distance. We recursively keep searching (always picking the child in the same subrectangle as the query point).

Now we have this “rule” of initially always searching the subrectangle the point is in. In principle, a closer point could be in the other subrectangle. A simple example is from the diagram drawn earlier in this page. If our point in question is around (7.01,5), then it is closer to (5,4), but that is in the other subrectangle (let’s pretend for a minute that (9,6) is not there…).

However, if we find a point in the right subrectangle that is closer than (7,2) is, then we need not search the left subrectangle we had skipped. There’s no way anything in there could be closer than our new candidate. (Not sure why this is true…)

The complexity is typically \(\lg N\), although in the worst case it is still \(N\) (examine all points).

Kd Tree

A Kd tree is an extension into \(K\) dimensions. Keep dividing into half spaces. Use the binary search tree as we did for 2D-trees, and cycle the dimensions as we did for 2D trees.

Very good for representing high dimensional data.

Applications