An undirected graph is defined by \((V, E)\) where \(V\) is a set of nodes and \(E\) is a set of edges (each edge is an unordered set of two nodes taken from \(V\)). It is referred to as a graph for short.
A directed graph is like an undirected graph, except that the edges point from one node to the other. As such, each edge is a tuple of nodes \((N_{1},N_{2})\) such that the edge is from \(N_{1}\) to \(N_{2}\). It is often referred to as a digraph for short.
For convenience, we’ll exclude self edges as well as multiple edges between the same nodes.
Properties & Definitions
Degree
The degree of a node in a graph is the number of edges connected to it. For a digraph, the indegree is the number of edges that are pointing to the node, and the outdegree is the number of edges that are pointing away from the node.
Let \(p_{k}\) be the fraction of nodes in the graph that have degree \(k\). The degree distribution of a graph can be visualized by making a histogram of the \(p_{k}\) values. In English, it is simply the number of nodes in a graph with a given degree, but then normalized to represent a probability. A byproduct of this is that it does form a probability mass function.
Paths & Distance
There exists a path of length \(k\) between two nodes \(a,b\) if there are \(k-1\) nodes you can insert between \(a,b\) such that there is an edge starting from \(a\) that goes through all the nodes to \(b\).
A path is simple if a node appears only once.
A path can be represented by the sequence of nodes the path traverses. Note that if the path is not simple, then the representation is not unique.
The distance between two nodes is the smallest \(k\) such that a path of length \(k\) exists between them. Note that there may be multiple paths of this distance in a graph - they need not be unique.
A cycle is a simple path that begins and ends at the same node.
A circuit also begins and ends at the same node, but it need not be simple.
An Eulerian tour is a cycle that traverses all the edges in the connected component exactly once. It can be shown that an Eulerian tour exists if and only if a graph is connected and the degree of each node is even.
Question: Describe an algorithm that gives an Eulerian tour?
Connectivity
A graph is connected if there is a path between every pair of distinct nodes. Note that this does not imply the graph is complete!
A connected component of a graph is a connected subgraph that is not a proper subgraph of another connected subgraph. In English: It is the largest possible subgraph containing a given node that is connected. The graph can be partitioned into connected components.
A digraph is strongly connected if there is a path between every pair of nodes (in both directions).
A digraph is weakly connected if its underlying undirected graph is connected.
Digraphs have the concept of strongly connected components: They are strongly connected but are not proper subgraphs of strongly connected subgraphs of the original digraph.
Bipartite Graphs
A graph is bipartite if its nodes can be partitioned into two disjoint and nonempty sets \(V_{1},V_{2}\) such that every edge connects a node from \(V_{1}\) to \(V_{2}\). There are no edges connecting nodes within these two sets.
The classical homework problem of connecting items from the first column to the second is an example.
Note that this does not mean every node has an edge.
Directed Acyclic Graph
A directed acyclic graph is a digraph with no cycles (although the underlying graph may have some).
Graph Representations
Adjacency List
An adjacency list for a graph consists of two columns. Each entry in the first column contains a node. Each entry in the 2nd column is a set of all the nodes connected to the node in the first column. If the graph is a digraph, then the first column only represents the node the edge begins from.
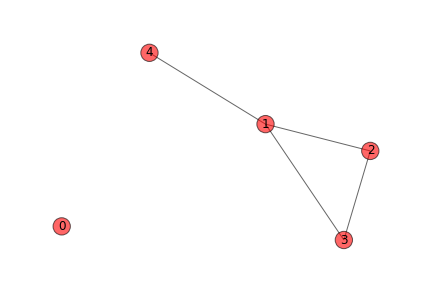
An example of an adjacency list of a digraph:
| Beginning Node | Ending Nodes |
|---|---|
| \(N_{1}\) | \(\{N_{2},N_{4}\}\) |
| \(N_{3}\) | \(\{N_{1}\}\) |
| \(N_{2}\) | \(\{N_{1},N_{3}\}\) |
This representation is useful if the graph is sparse.
This corresponds to the following graph:
Adjacency Matrix
An adjacency matrix \(A\) has \(A_{ij}=1\) if and only if the nodes \(i\) and \(j\) are connected by an edge. Otherwise the value is 0.
In a digraph, it is 1 if and only if the edge goes from node \(i\) to \(j\).
The matrix for an undirected graph is symmetric.
This representation is useful if the graph is dense.