Mincut Problem
An s-t cut is a cut with \(s\) in one set and \(t\) in the other. Call the sets \(A\) and \(B\).
Given a digraph, with positive edge weights (referred to as capacity), and a source \(s\) and target node \(t\), we define the capacity of the cut to be the sum of the capacities of the crossing edges from \(A\) to \(B\) (note: the edges are directional - we don’t care about crossings from \(B\) to \(A\)).
The goal is to find the minimum capacity cut. This is useful in isolating a group of people (e.g. if you want to cut off the Internet).
Max Flow Problem
Assign to each edge not only a capacity, but a flow, such that the flow is non-negative, but not greater than the capacity. This assignment is called the \(s-t\) flow.
We require that for each node (except \(s\) and \(t\)), the sum of the flows for incoming edges must equal the outgoing sum (no sources or sinks other than the two nodes).
The value of a given \(s-t\) flow is the sum of all the flows into \(t\).
(We assume no edges point into \(s\), or out of \(t\)).
The problem is to find the flow that maximizes this number.
A use case is if one wants to get the maximum amount of aid to a region.
Duality
The mincut and max flow problems are actually duals of one another.
Ford-Fulkerson Algorithm
Set the flow to be 0 for all edges.
An augmenting path is a path from \(s\) to \(t\) such that:
- You can increase flow on forward edges (none of the edges in the path is at capacity).
- You can decrease flow on a backward edge (none of the backward edges has 0 flow).
What is a backward edge? If we have an edge from \(u\) to \(v\), a backward edge is an imaginary one from \(v\) to \(u\) (need not exist in the network). Conceptually, it just means that if the edge from \(u\) to \(v\) has some flow, we can reduce that flow in order to clear up bottlenecks and allow flow from other nodes.
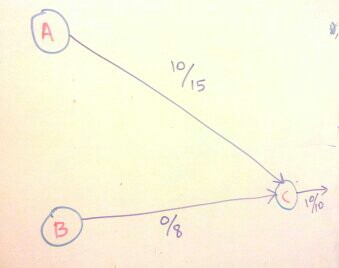
In the image shown, the capacities are 15, 8 and 10, and the flows are 10, 0 and 10. So all that is flowing from A to C is flowing out of C and there’s no room to add anything from B.
If we wanted to, we could add, say, 6 from B to C, but then we’d need to reduce the flow from A to C by the same amount (bringing it to 4). In this case, the edge from C to A is a backward edge. It’s as if we’re inserting 6 from B, and taking it out of C into A.
The algorithm is that as long as an augmenting path exists, use it to increase the overall flow. At some point you won’t be able to find an augmenting path (all possible paths either have a full edge or an empty backward edge that you cannot use to reroute).
Questions:
- How can we compute a mincut from this?
- How can we find augmenting paths?
- If the algorithm terminates, is the flow maximized?
- Does the algorithm always terminate? (Guaranteed if the edge weights are integers)
Max Flow Mincut Theorem
The net flow across a cut \((A,B)\) is the sum of the flows of the crossing edges from \(A\) to \(B\) minus the sum in the other direction.
Flow Value Lemma: Let \(f\) be the flow of a digraph and \((A,B)\) be any cut. Then the net flow across \((A,B)\) equals the value of \(f\).
This can be seen by realizing that there are no sources and sinks other than the \(s\) and \(t\) nodes. More formally, prove by induction. Let \(B=\{t\}\) Then it’s trivially true. This is the base case. For the inductive step, if it’s true for a given \((A',B')\), then moving a node from one set to the other cannot alter the overall flow from \(A'\) to \(B'\). I’m handwaving here, but thinking formally, if a node \(u\) moves from \(B'\) to \(A'\), then there are two cases: If none of the original crossing edges involved \(u\), and if some did. In the former, all the edges involving \(u\) become (new) crossing edges, but their sum must be 0 (from equilibrium). In the latter case, let \(\{a_{i}\}\) be all the crossing edges from \(A\) to \(B\) involving \(u\), and \(\{b_{i}\}\) be all the crossing edges within \(B\) involving \(u\). Once you move \(u\) to \(A\), the crossing edges involving \(u\) now become \(\{b_{i}\}\). But from equilibrium, the sum of all flows in edges in both sets must be the same.
Weak Duality: The value of flow \(f\) is less than the capacity of any cut \((A,B)\).
Theorem: A flow \(f\) is a max flow iff there are no augmenting paths. The value of the max flow is the capacity of the mincut.
Proof: It follows from the equivalence of these 3 statements:
- There exists a cut whose value equals the flow of \(f\).
- \(f\) is a max flow.
- There is no augmenting path with respect to \(f\).
1 implies 2: If such a cut exists, then the value of any other flow must be less than the capacity of this cut! Hence, this is the maximum possible flow.
2 implies 3 from the contrapositive: If a path exists, then we can increase the flow.
3 implies 1: Let \((A,B)\) be a cut such that all the nodes connected to \(s\) in \(A\) have no full forward or empty backward edges. \(t\) must be in \(B\) (as there is no augmented path). Now the capacity of this cut is the net flow across the cut as all crossing forward edges are full (backward edges are empty). But this is the flow of \(f\) by the flow-value lemma.
Computing the mincut From the Max Flow
Let \(A\) be the set of all nodes connected to \(s\) with no full forward or empty backward edges. This cut forms the mincut.
Question: Why?
Analysis
If we assume all the capacities and flows are integers, then the number of augmentations is bounded above by the value of the max flow (as increments to the flow can only be in integral amounts). This guarantees termination of the algorithm.
| Augmenting Path | Max Number of Augmenting Paths | Implementation |
|---|---|---|
| Shortest Path | \(0.5NM\) | BFS |
| Fattest Path | \(M\ln(MU)\) | Priority Queue |
| Random Path | \(MU\) | Randomized Queue |
| DFS Path | \(MU\) | Stack (DFS) |
No proof of these bounds given, and in practice is often a lot lower. \(U\) is the maximum capacity?
Implementation Details
It’s convenient to consider the residual graph. Construct this graph as follows:
- For all forward edges that are not at full capacity, replace with an edge whose weight is the remaining capacity. And create an edge in the opposite direction with the weight of the flow of the forward edge.
- For all full forward edges, do as above but as the forward edge weight is 0, simply don’t draw that edge.
- Similarly, if the flow is 0 in the original graph, don’t bother putting a reverse edge of weight 0.
In this residual graph, simply find a directed path from \(s\) to \(t\). Here you can use BFS, etc.
In practice, the push-relabel method works quite well.
Applications
Bipartite Matching Algorithm
As an illustration, say you have \(N\) people, applying to \(N\) companies. Each company gives some people job offers. Is it possible that each person gets a job and each company gets a new employee?
Converting this into a max flow problem is straightforward. Introduce nodes \(s\) and \(t\), and connect all employees to \(s\), and all companies to \(t\). Let the capacities of these edges be 1. Now connect an employee to a company if the company offered them a job, and let the capacity be infinite.
Now any augmenting path must go through exactly one employee and exactly one company. Furthermore, as the capacity is 1, an employee cannot be part of 2 augmenting paths (same goes for the companies).
If the max flow is \(N\), then you’ve found a perfect matching. If it is less than \(N\), then you cannot get a perfect matching.
Baseball Elimination Problem
Say you have \(N\) teams. Each has won \(w_{i}\) games, and each has \(r_{i}\) games left to play. The question is, can we prove that some team has no chance of coming on top of the league (assume a point per win and no ties)?
Let’s take the example of a league with 5 teams (numbered from 0 to 4) and we’re considering team 4. Look at the graph below:
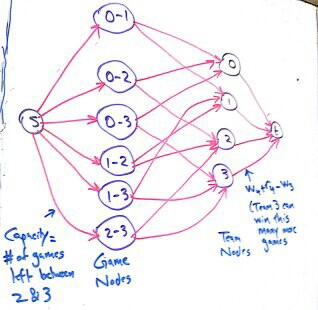
Note the following:
- The capacity from the source to the game nodes is the number of games remaining between those 2 teams.
- The edges from the games to the teams has infinite capacity.
- The capacity from the teams to the target is the number of more games team 4 can win than team \(i\). This is assuming team 4 wins all the remaining games. In other words, team \(i\) has to win this many more games to tie with team 4 if team 4 wins all remaining games.
Team 4 is not eliminated if and only if all edges from \(s\) are full.
Assume we have a max flow. If all edges leaving from \(s\) are full (which means all remaining games have been played), then that means the edges going to the sink have not “overflowed” - they either have some capacity or are all full. If they have some capacity, that means those teams did not beat team 4 in number of points and lag behind. If the capacity is 0, it means they tied with team 4.
Conversely, assume some edges pointing from \(s\) are not full but we have maxflow. This can only happen if some edges to \(t\) are full (those teams are tied with team 4). As an example, if the edge from \(s\) to \(0-1\) is not full, then the edges from 0 and 1 to \(t\) must be full (otherwise we have an augmenting path). This means both teams 1 and 0 are tied with 4, but they still have some more games to play with each other. In the next game, whoever wins will be ahead of team 4. Hence, if team 4 is not eliminated, all edges from \(s\) must be full.
What if \(w_{4}+r_{4}-w_{i}\) is negative to begin with? Well, we can’t have negative capacity. But in words, this simply means that team \(i\) already has more wins than team 4 can possibly achieve, and so if our graph has a negative capacity, then team 4 is eliminated from the get go.